# 散点图
# 何时使用
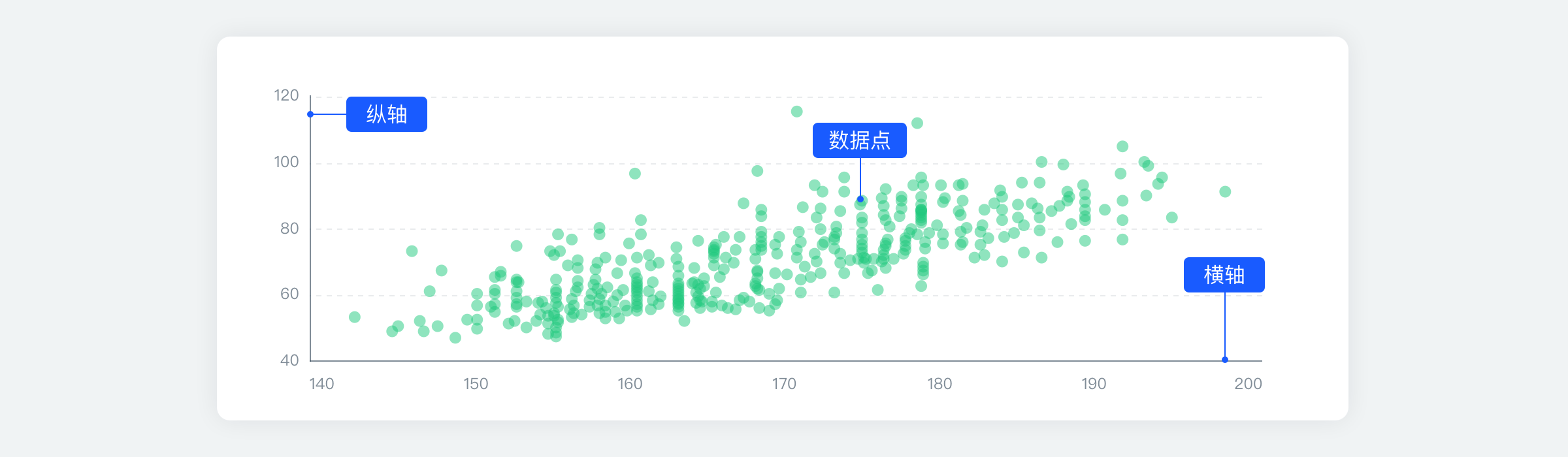
散点图在直角坐标系显示数据的两个变量(X、Y)之间的关系。它将所有的数据以点的形式展现在直角坐标系上,以显示变量之间的相互影响程度,点的位置由变量的数值决定,适合用于在不考虑时间的情况下比较大量的数据点。散点图通常用来识别两个变量之间的相关性或用来观察它们的关系,从而发现某种趋势,对于查找异常值或理解数据分布也很有效。
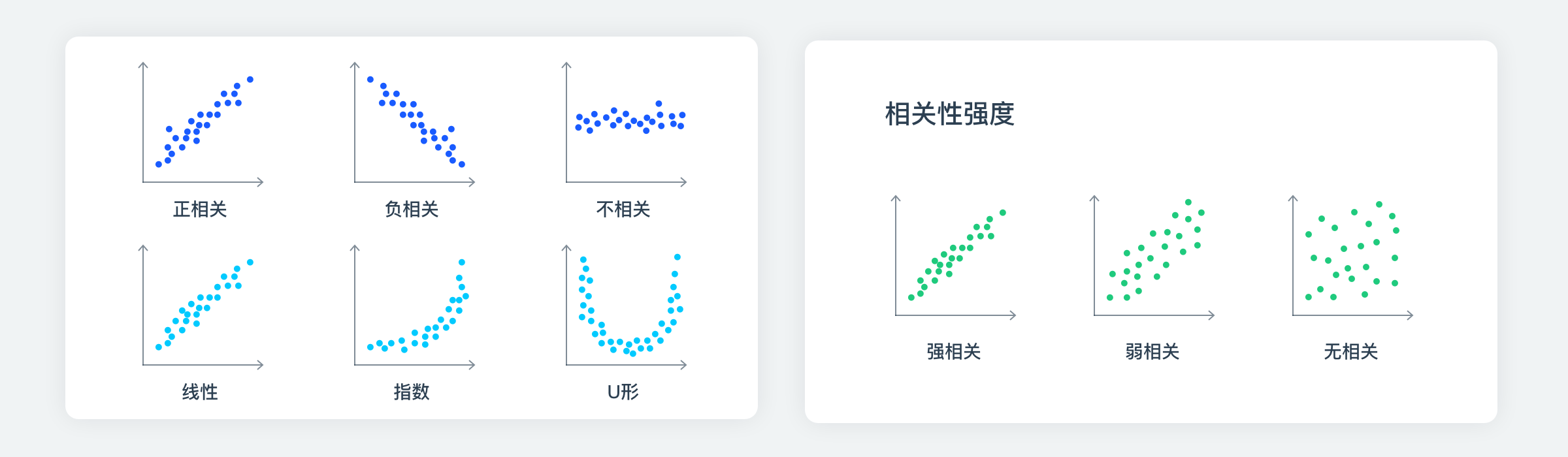
通过观察散点图上数据点的分布情况,我们可以推断出变量间的相关性。如果变量之间不存在相互关系,那么在散点图上就会表现为随机分布的离散的点;如果存在某种相关性,那么大部分的数据点就会相对密集并以某种趋势呈现。数据的相关性主要分为:正相关(两个变量值同时增长)、负相关(一个变量值增加另一个变量值下降)、不相关、线性相关、指数相关等,表现在散点图上的大致分布如下图所示。那些离点集群较远的点我们称为离群点或者异常点。
注意: 变量之间的相关性并不等同于确定的因果关系,也有可能存在另一个变量在影响着结果。
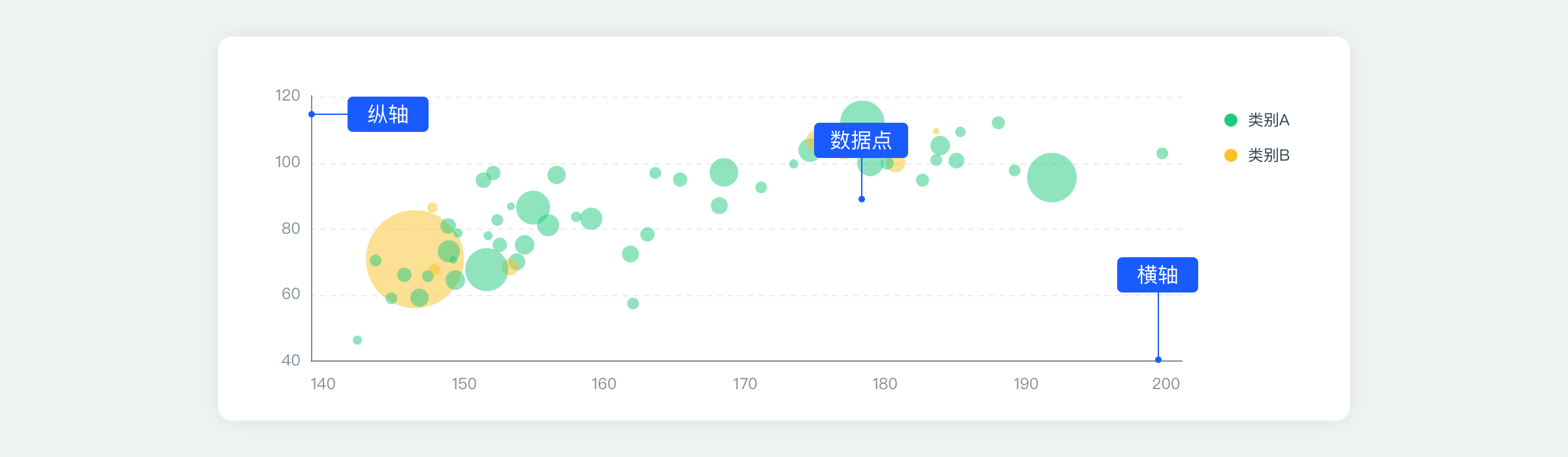
气泡图是一种多变量图表,是散点图的变体,也可以认为是散点图和百分比区域图的组合,它增加了第三个数值即气泡大小的变量。在气泡图中,较大的气泡表示较大的值。可以通过气泡的位置分布和大小比例,来分析数据的规律。
# 图表属性
- 图表血缘: 统计图表 - 散点图类
- 视觉通道: 颜色、位置、大小
- 分析目的: 比较、分布
# 图表故事
- 这两个度量是否相关?相关程度如何?
- 与其他度量相比,某些度量是否更加相关?
- 这些度量的相关程度如何?
# 使用建议
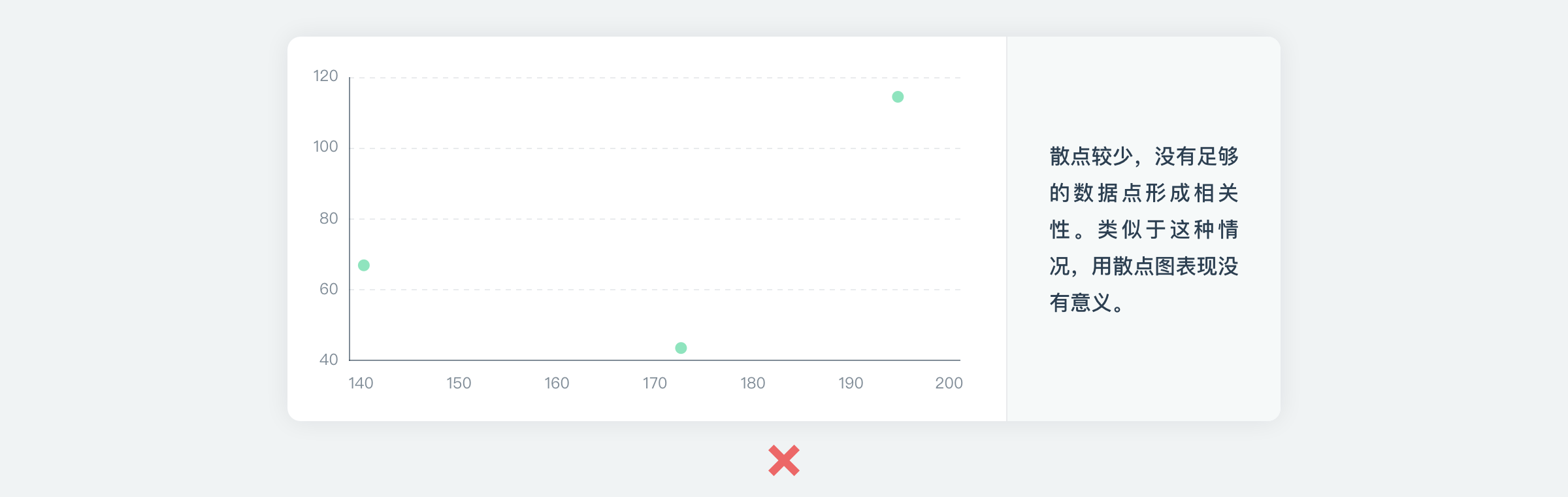
1、如果一个散点图没有显示变量之间的任何关系,那么或许该图表类型不是此数据的最佳选择。
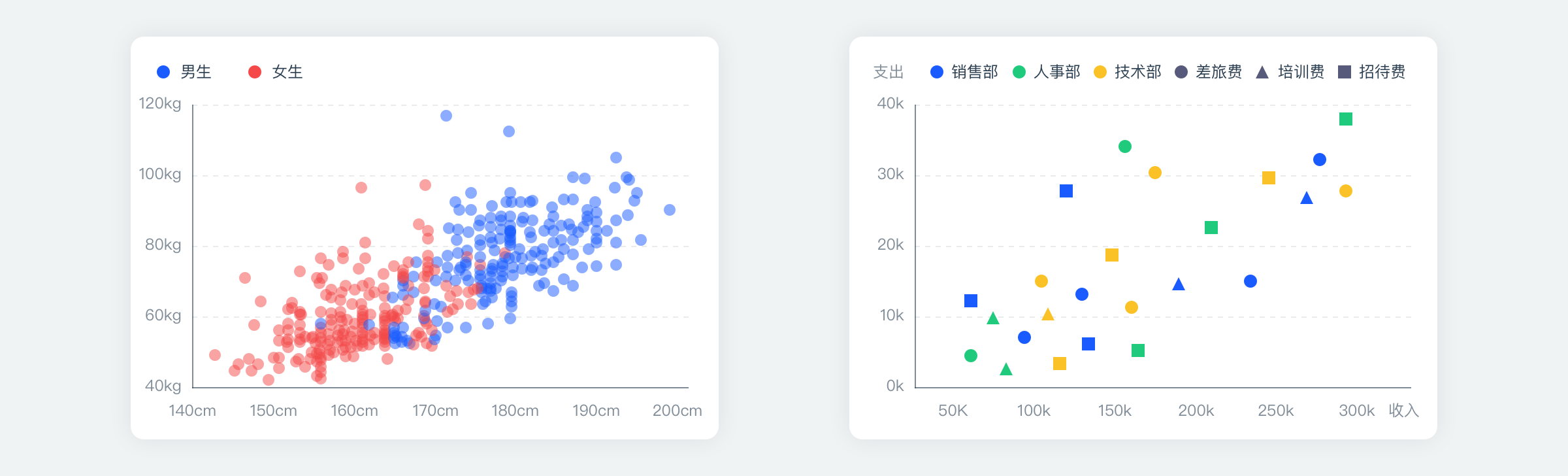
2、如果数据包含不同系列,可以给不同系列使用不同的颜色,并增加图例标注出颜色代表的含义;还可以分别添加每个系列平均值的辅助线,有助于更好的理解数据的分布情况。
在观察两个变量之间的关系时,趋势线是非常有用的,趋势线的形状走向解释了两个变量之间的关系类型,还可以用来预测未来的值。但需要注意的是趋势线最可只能使用两条,以免干扰正常的数据的阅读。
3、如果数据之间没有相关性,那么绘制不相关的散点图是没有意义的。
4、当数据具有 3 个序列、特征及相关值,使用气泡图是一个不错的选择。
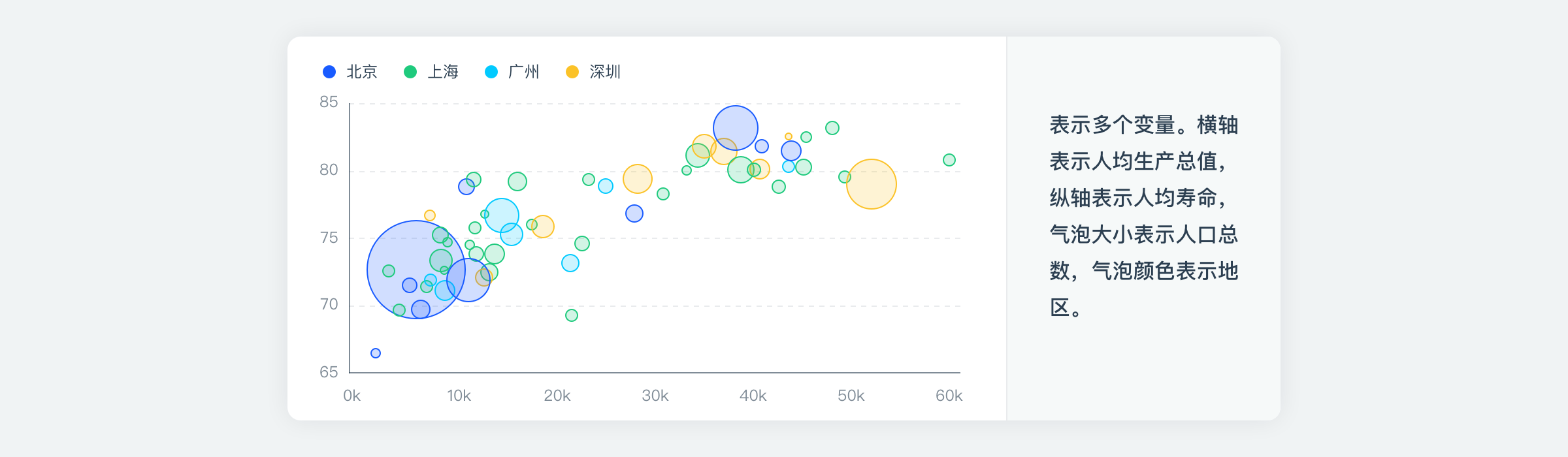
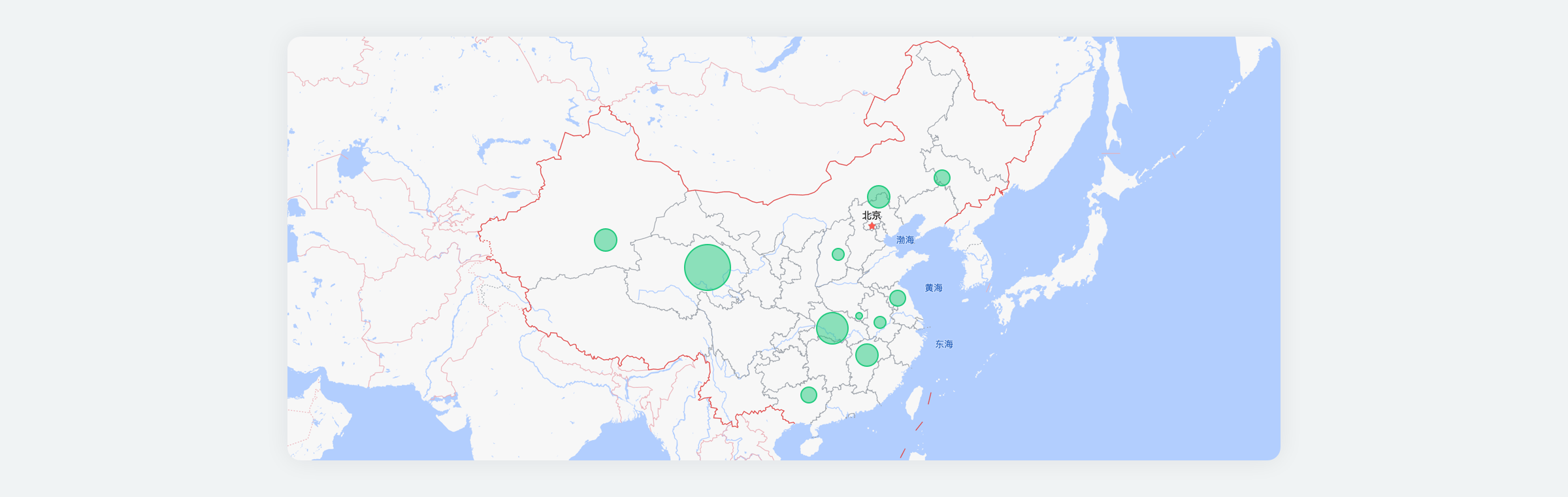
5、气泡图还经常用于和地图结合,其中 X 轴和 Y 轴是经度和纬度的数据定位,气泡的大小可以表明该位置数量的多少。